An Introduction to Regenerative Electromagnetic Design

Chapter I: Introduction

Regenerative Electromagnetic Design (RED) applies electromagnetic engineering principles to minimize interference and bio-incompatibility and actively supports systemic resilience, biological coherence, and energy renewal. RED aligns fields with natural rhythms and quantum symmetries to foster technological and ecological health. It moves beyond mitigation into active field harmonization and regenerative feedback.

Chapter II: Foundational Quantum Mechanisms

To rigorously ground regenerative electromagnetic design in physics, we explore five quantum phenomena, including supporting equations and symbol definitions. These mechanisms are essential to understanding how electromagnetic fields can be structured for coherence, resonance, and regeneration.

Quantum Coherence and Decoherence

Quantum coherence supports enhanced functionality in both biological and synthetic systems.

Decoherence can be minimized via shielding or constructive field alignment.

Equation:
ρ = \[∣ψ1∣2,ψ1ψ2∗\[|ψ₁|², ψ₁ψ₂*\[∣ψ1∣2,ψ1ψ2∗, ψ2ψ1∗,∣ψ2∣2ψ₂ψ₁*, |ψ₂|²ψ2ψ1∗,∣ψ2∣2] → \[∣ψ1∣2,0\[|ψ₁|², 0\[∣ψ1∣2,0, 0,∣ψ2∣20, |ψ₂|²0,∣ψ2∣2]

Symbol Definitions:

ρ (rho): Density matrix, representing a quantum system's statistical state.
ψ₁, ψ₂ (psi): Amplitudes of quantum wavefunctions for two basis states.
|ψ₁|², |ψ₂|²: Probability of the system being in state ψ₁ or ψ₂, respectively.
ψ₁ψ₂*: Coherence term between the two states (ψ₂* is the complex conjugate of ψ₂).
The transformation (→) represents decoherence, where off-diagonal terms decay due to environmental interaction.

Design Application: Use superconducting materials, nonlocal quantum entanglement channels, or low-frequency EM resonance chambers to preserve coherence in communication and biological systems.

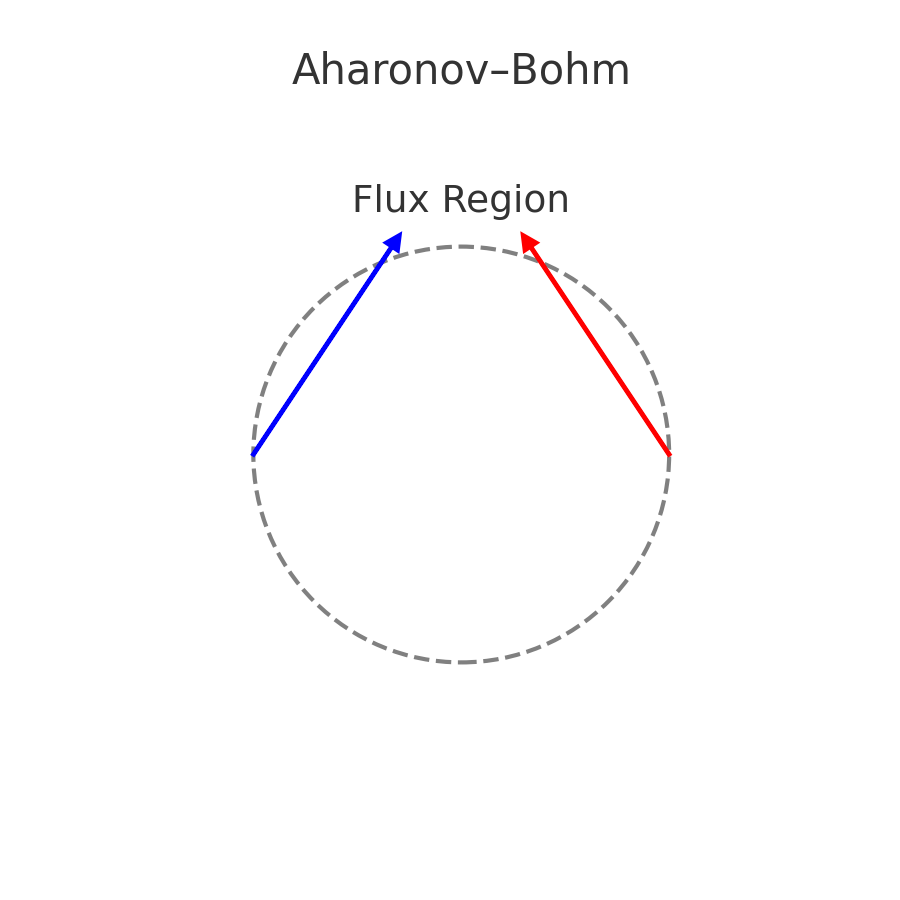
Aharonov–Bohm Effect

Demonstrates that the electromagnetic potential, even in regions where the electric field and magnetic field, can affect a quantum particle’s phase:

Equation:
Δφ = (q / ħ) ∮ A · dl

Symbol Definitions:

Δφ (delta phi): Quantum phase shift due to the presence of a vector potential.
q: Electric charge of the particle (e.g., electron).
ħ (h-bar): Reduced Planck's constant, ħ = h / 2π.
A: Electromagnetic vector potential.
dl: Differential path element along the particle's loop.
∮ A · dl: Line integral of the vector potential around a closed loop.

Design Application: Employ field-excluding geometries like magnetic vector potential wells to guide quantum particles or control interference in sensor networks.

Casimir Effect and Vacuum Field Engineering

The Casimir force arises due to quantum zero-point energy differences between closely spaced conducting plates:

Equation:
F = (π²ħc) / (240d⁴) × A

Symbol Definitions:

F: Casimir force between two uncharged, parallel conducting plates.
π: Pi, a mathematical constant ≈ 3.1416.
ħ (h-bar): Reduced Planck's constant.
c: Speed of light in a vacuum.
d: Distance between the plates.
A: Area of each conducting plate.

Design Application: Use nanoscale gap structures to harness Casimir effects for micro-power regeneration or dynamic field attenuation.

Spintronics and Magnetic Spin States

Quantum spin states can represent binary or analog information and are governed by the Pauli matrices:

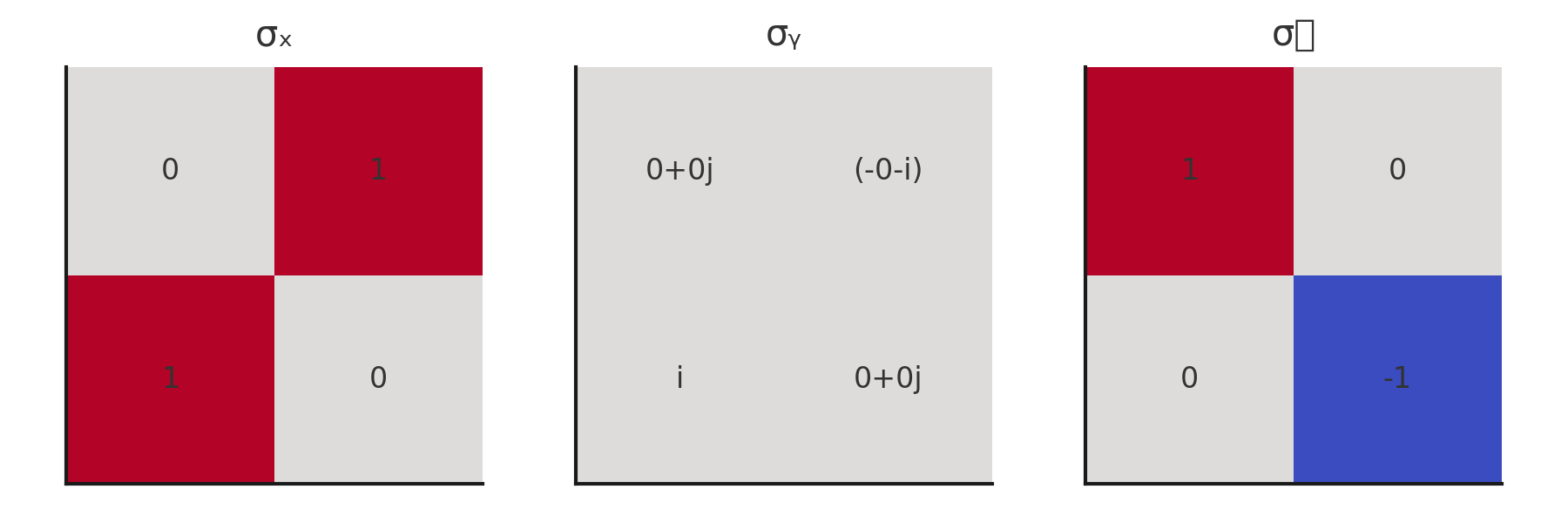
Pauli Matrices:

σₓ = \[0,1\[0, 1\[0,1, 1,01, 01,0]
σᵧ = \[0,−i\[0, -i\[0,−i, i,0i, 0i,0]
σ𝓏 = \[1,0\[1, 0\[1,0, 0,−10, -10,−1]

Symbol Definitions:

σₓ, σᵧ, σ𝓏: Pauli matrices representing quantum spin operators along the x, y, and z axes.
i: Imaginary unit, where i² = -1.
These matrices operate on spinor wavefunctions (quantum states with spin), and are fundamental in quantum mechanics and quantum computing.

Design Application: Implement ferromagnetic lattice structures for energy-efficient, regenerative logic gates or shielding that adapts to spin alignments.

Quantum Entanglement and Field Resonance

Entangled quantum systems share nonlocal correlations:

Entangled State Equation:
|Ψ⟩ = 1/√2 (|01⟩ + |10⟩)

Symbol Definitions:

|Ψ⟩ (Psi ket): The entangled state of a two-particle quantum system.
|01⟩, |10⟩: Tensor product basis states of two qubits — particle 1 in state 0 and particle 2 in state 1, and vice versa.
1/√2: Normalization factor ensuring the total probability equals 1.
This equation describes a Bell state, showing perfect quantum correlation between two entangled particles, regardless of distance.

Design Application: Create phase-locked field resonance systems where entangled signal sources synchronize across large distances — e.g., in distributed regenerative antenna arrays.

III. Proposed Topologies for Regenerative EM Infrastructure

Toroidal Field Circuits

Closed-loop, field-conserving circuits that mimic natural magnetic containment (e.g., Earth’s magnetosphere, plasma toroids). Reduces field leakage and interference.

Fractal-Resonant Structures

Nested geometries that promote broadband absorption, field scaling, and bio-compatibility. Excellent for antenna, shielding, and space-field integration.

Scalar-Phase Interferometry Networks

Networks using phase-cancelled EM fields to neutralize disruptive radiation while retaining signal function in core systems.

Piezo-Magneto-Electric Lattices

Systems that convert EM to mechanical or electrochemical regeneration, potentially self-balancing under fluctuating loads or geofield conditions.

Bio-Integrated Circuit Topologies

Circuits whose EM patterns are entrained to biological rhythms (e.g., Schumann resonance harmonics), reducing conflict with cellular processes.

IV. Applications

Human-Optimized Buildings
EMF systems are designed to promote circadian alignment, cognitive clarity, and cardiovascular coherence.
EM-Quiet Infrastructure
Data centers, hospitals, and smart cities with non-disruptive electromagnetic footprints.
Resilient Energy Transfer Systems
Wireless power systems or VFDs with embedded field harmonization and reduced harmonic radiation.
Quantum-Safe Digital Communications
Topologically optimized signal transmission that resists decoherence and preserves data integrity in dense EM environments.
Medical Implants and Sensors
Regenerative field coupling to tissues using constructive interference principles and non-ionizing signaling.

IV. Challenges

Material Constraints
Lack of commercially available materials that maintain coherence or support toroidal topologies without losses.
Regulatory Frameworks
Standards are designed around exposure limits, not field enhancement or regeneration. Policy lag will limit adoption.
Testing Methodologies
Most EMC/EMI testing tools measure interference, not constructive field properties or regenerative feedback loops.
Scientific Conservatism
Quantum-coherent field design is often labeled pseudoscientific unless rigorously grounded in lab data.

V. Opportunities

Establishing New Standards
Define a Regenerative Electromagnetic Compatibility (rEMC) framework — not just “do no harm,” but do measurable good.
Open-Source Design Topologies
Publish or license fractal, toroidal, and scalar EM circuit architectures for regenerative integration.
Bio-AI Co-evolution Systems
Infrastructure that enables AI systems to operate optimally in biologically regenerative fields, avoiding cross-influence degeneration.
Cross-Disciplinary Research Consortia
Physics, electrical engineering, neuroscience, and architecture united under regenerative EM design goals.

Note: Diagrams showing field loops, Casimir gaps, and spin alignments are separate upon request.

[Further chapters will explore Topological Architectures, Biological Integration, and Real-World Systems Design.]

References

Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information.
Aharonov, Y., & Bohm, D. (1959). Significance of Electromagnetic Potentials in the Quantum Theory. Physical Review, 115(3), 485–491.
Casimir, H. B. G. (1948). On the Attraction Between Two Perfectly Conducting Plates. Proceedings of the Royal Netherlands Academy of Arts and Sciences.
Wolf, S. A., et al. (2001). Spintronics: A Spin-Based Electronics Vision for the Future. Science, 294(5546), 1488–1495.
Aspect, A., Dalibard, J., & Roger, G. (1982). Experimental Test of Bell's Inequalities Using Time‐Varying Analyzers. Physical Review Letters, 49(25), 1804–1807.